Un miliardar ofera 1 milion de dolari pentru cine rezolva aceasta ecuatie
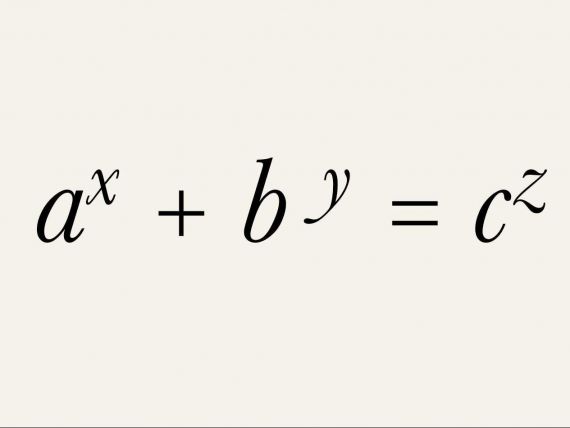
Matematicianul si bancherul texan Andrew Beal pune la bataie un premiu de un milion de dolari pentru cel care va reusi sa demonstreze o ipoteza pe care el a descoperit-o in 1993, transmite Associated Press, citata de Business Insider.
Cu sprijinul Societatii Americane de Matematica, premiul de un milion de dolari va fi acordat primei persoane care va putea sa demonstreze ipoteza lui Beal, o ramificatie a cunoscutei teoreme a lui Fermat, care a fost demonstrata in 1994, de catre Andrew Wiles.
Ultima teorema a lui Fermat a ramas nerezolvata timp de sute de ani. Potrivit acesteia, nu exista trei numere intregi pozitive a, b, c, care sa satisfaca relatia ax + bx = cx, atunci cand x, numar intreg, este mai mare decat doi. Desi acest lucru pare la prima vedere evident, este de fapt foarte greu de dovedit.
Andy Beal lucra la teorema lui Fermat, cand a dat peste o alta problema. La vremea respectiva, folosea computerul pentru a analiza ecuatii similare, cu exponenti diferiti. Asa ca ipoteza lui Beal este oarecum inrudita. Daca a, b, c , x, y, z sunt numere intregi pozitive si x, y, z sunt mai mari decat 2, atunci ax + by = cz este valabila numai cand a, b si c au un factor comun (de exemplu daca ar fi vorba de 8, 6 si 10, care il au pe doi drept factor comun).
Beal si-a contactat colegii academicieni pentru a se convinge ca problema era, intr-adevar, una noua, si a stabilt apoi un premiu impreuna cu AMS, pentru persoana care va face demonstratia. Asa ca cel care gaseste calea de a demonstra sau, dimpotriva, de a contrazice ipoteza lui Beal, primeste un milion de dolari.
Mai multe informatii despre premiu gasiti aici:
http://www.math.unt.edu/~mauldin/beal.html
http://www.ams.org/profession/prizes-awards/ams-supported/beal-prize .
 VOYO
VOYO

 RON
RON RON
RON RON
RON RON
RON (P) iBani. Piața imobiliară după majorarea TVA. Sfaturi pentru cei interesați să cumpere o locuință nouă
(P) iBani. Piața imobiliară după majorarea TVA. Sfaturi pentru cei interesați să cumpere o locuință nouă
 ”Incont”, site-ul Știrile Pro TV de informații economice și educație financiară, a devenit ”iBani”
”Incont”, site-ul Știrile Pro TV de informații economice și educație financiară, a devenit ”iBani”  România, departe de zona euro. Analist: Probabil ne ducem spre 2030 cu adoptarea monedei unice
România, departe de zona euro. Analist: Probabil ne ducem spre 2030 cu adoptarea monedei unice
 Popa, CFA România: Într-o lume fără pensii private ar trebui să ne aşteptăm la o pensie de 32% din ultimul salariu
Popa, CFA România: Într-o lume fără pensii private ar trebui să ne aşteptăm la o pensie de 32% din ultimul salariu
 Siemens Energy anunţă concedieri masive pentru a-şi majora profitul. Compania are mii de angajați în România
Siemens Energy anunţă concedieri masive pentru a-şi majora profitul. Compania are mii de angajați în România
 Cu trenul de la Paris la Viena sau de la Zurich la Barcelona. Pandemia reînvie cursele feroviare de noapte în Europa
Cu trenul de la Paris la Viena sau de la Zurich la Barcelona. Pandemia reînvie cursele feroviare de noapte în Europa  (P) De ce aleg românii să joace la pariuri
(P) De ce aleg românii să joace la pariuri
 (P) Tot ce trebuie să știi despre vigneta Ungaria și prețul acesteia
(P) Tot ce trebuie să știi despre vigneta Ungaria și prețul acesteia
 Digitalizarea departamentului HR - un subiect în trend chiar și pentru companiile de IT
Digitalizarea departamentului HR - un subiect în trend chiar și pentru companiile de IT
 Huawei dezminte zvonurile privind vânzarea brandurilor premium de smartphone P şi Mate
Huawei dezminte zvonurile privind vânzarea brandurilor premium de smartphone P şi Mate  Cum vom lucra în 2021: 60% dintre companii vor să reînceapă munca de la birou din luna martie. Mai mult de jumătate au tăiat programele de training şi pe cele de wellbeing
Cum vom lucra în 2021: 60% dintre companii vor să reînceapă munca de la birou din luna martie. Mai mult de jumătate au tăiat programele de training şi pe cele de wellbeing  Două treimi din forţa de muncă existentă la nivel global lucrează de acasă, însă unul din trei angajaţi folosește propriul calculator pentru a-şi desfăşura activitatea
Două treimi din forţa de muncă existentă la nivel global lucrează de acasă, însă unul din trei angajaţi folosește propriul calculator pentru a-şi desfăşura activitatea 
 Invață să ții sub control cheltuielile de sărbători. Cum funcționează cardul de cumpărături
Invață să ții sub control cheltuielile de sărbători. Cum funcționează cardul de cumpărături  Moneda euro la 20 de ani. Cea mai importantă realizare macro-economică a secolului trecut a supraviețuit marii crize mondiale, dar rămâne un colos handicapat de propriile slăbiciuni
Moneda euro la 20 de ani. Cea mai importantă realizare macro-economică a secolului trecut a supraviețuit marii crize mondiale, dar rămâne un colos handicapat de propriile slăbiciuni
 UE pregătește măsuri de urgență, în cazul unui ”no deal” cu Londra, din ianuarie. Domeniile vizate: pescuitul şi transportul rutier şi aerian
UE pregătește măsuri de urgență, în cazul unui ”no deal” cu Londra, din ianuarie. Domeniile vizate: pescuitul şi transportul rutier şi aerian
 Explozie la gazoductul din Ucraina care asigura gazele pentru Europa. Ce se întâmplă cu livrările de gaze rusești spre continent
Explozie la gazoductul din Ucraina care asigura gazele pentru Europa. Ce se întâmplă cu livrările de gaze rusești spre continent




 RSS
RSS